Цель: открытие учащимися свойств параллелограмма в ходе эксперимента при работе в виртуальной среде «Живая математика»; применение свойств параллелограмма в ходе решения задач.

Оборудование:

• компьютер учителя;
• нетбуки для учащихся;
• мультимедийный проектор, экран;
• документ-камера,
• тетради на печатной основе по геометрии для 8 класса (у каждого учащегося).

Структура урока:

1. Организационный момент.
2. Постановка цели урока.
3. Актуализация знаний учащихся в ходе проверки домашней работы.
4. Решение задач на готовых чертежах с целью подготовки к изучению нового материала (устно).
5. Изучение нового материала, экспериментальная работа.
6. Закрепление изученного материала в ходе решения задач в рабочих тетрадях на печатной основе.
7. Постановка домашнего задания.
8. Подведение итогов урока.      

Ход урока

1. Организационный момент

Проверяется подготовленность классного помещения и готовность учащихся к уроку.
 

2. Постановка целей урока

Данный урок является уроком изучения нового материала по теме «Параллелограмм и его свойства». На уроке в ходе исследовательской работы в виртуальной среде «Живая математика» учащиеся экспериментально выводят свойства параллелограмма. А также приобретают практические навыки применения знаний по теме в стандартных условиях в ходе решения задач в рабочих тетрадях на печатной основе.
 

3. Актуализация знаний учащихся в ходе проверки домашней работы

Решение задач домашней работы проверяется с помощью  документ-камеры.
 

4. Решение задач на готовых чертежах с целью подготовки к изучению нового материала (устно)

Учащиеся решают устно задачи на готовых чертежах (чертежи заранее заготовлены на доске).

Работа проводится с целью подготовки к изучению нового материала. Учащимся дается 1-2 минуты на обдумывание задачи, а затем заслушиваются различные варианты решений, обсуждается, какое из решений наиболее верное, рациональное.

Задачи

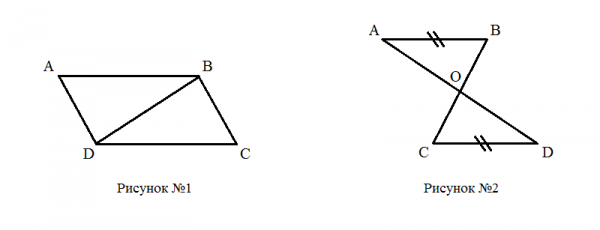
1. Дано: АВ || CD,  BC ||  AD (рисунок 1)
   Доказать:  ВС = АD,
2. Дано АВ || CD, AB = CD (рисунок 2)
   Доказать: О – середина AC и BD.

5. Изучение нового материала, экспериментальная работа

Учащиеся работают с нетбуками в виртуальной среде «Живая математика».

• Вводится понятие параллелограмма.

• Исследовательская работа в виртуальной среде «Живая математика», в ходе которой учащиеся экспериментально выводят свойства параллелограмма. Они производят измерения отрезков и углов с помощью инструментария программы «Живая математика». Учащиеся сопровождают решение каждой задачи анализом того, насколько формулируемые ими положения выдерживают вариации исходных элементов чертежей, полученных из исходных, с помощью команды Анимация.

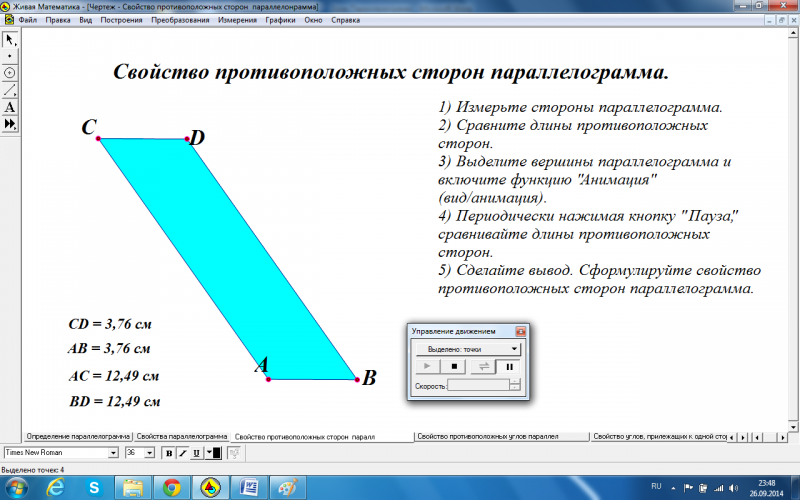
• Первый этап: учащиеся измеряют стороны фигуры с помощью выбора вкладки Измерения горизонтального меню.

• Второй этап: воспользовавшись командой Анимация (меню Вид)  учащиеся наблюдают, анализируют и делают выводы, каким образом меняются измеренные ими величины. Учитель контролирует правильность умозаключений и формулировок свойств параллелограмма, предложенных учащимися.

• Далее учащиеся работают в виртуальной среде «Живая математика», следуя четко инструкции, записанной справа на каждом слайде презентации в программе под руководством учителя (выполняя первый и второй этапы). Смотри Приложение 1.
   

6. Закрепление изученного материала в ходе решения задач в рабочих тетрадях на печатной основе.

Задачи № 8, 9, 10  учащиеся решают самостоятельно, затем один из учащихся читает свое решение, остальные проверяют свое решение, исправляют ошибки отвечающего.

Задача № 8

В параллелограмме ABCD найдите: а) стороны, если ВС на 8 см больше стороны АВ, а периметр равен 64 см; б) углы, если

Решение.

а) По свойству параллелограмма АВ = CD, ВС =  АD  и . По условию Р_ABCD = 64 см, следовательно, 2 (АВ + ВС) = 64 см, откуда АВ + ВС = 32 см, но ВС на 8 см больше АВ, поэтому АВ + АВ + 8 см = 32 см, откуда АВ = 12 см, ВС = 12 см + 8 см = 20 см.

б) По условию , а так как , то 

Задача № 9

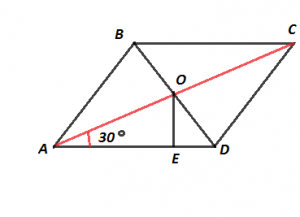
В параллелограмме АВСD диагональ АС, равная 24 см, образует со стороной АD угол в 30^о, о – точка пересечения диагоналей АС и ВD, . Найдите длину отрезка ОЕ.

Решение.

Диагонали параллелограмма точкой пересечения делятся пополам, поэтому АО = ОС = 12 см. Треугольник AOE – прямоугольный с гипотенузой АО и острым углом А, равным 30°. Поэтому катет ОЕ, лежащий против угла в 30^о, равен ½ АО, т.е. ОЕ = ½ * 12 см = 6 см.

Ответ: 6 см.

Задача №10.

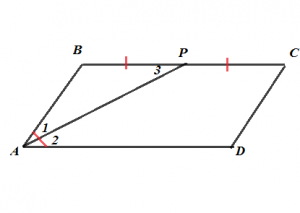
Биссектриса угла АВ параллелограмма АВСD пересекает сторону ВС в точке Р, причем ВР = РС. Найдите стороны параллелограмма, если его периметр равен 54 см.

Решение.

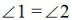• , так как луч АР – биссектриса угла А, 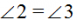, так как эти углы накрест лежащие  при пересечении параллельных прямых AD и ВС секущей АР. Следовательно,  .
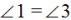• Треугольник АВР – равнобедренный, так как его углы 1 и 3 равны, поэтому АВ = ВР.
• По условию ВР = РС, следовательно, ВС = 2 * ВР = 2 * АВ.

Итак, Р _ABCD = 2(АВ + 2 * АВ) = 6 * АВ.

Так как периметр параллелограмма равен 54 см, то 6 * АВ = 54 см, откуда АВ = 9 см и ВС = 18 см.

Ответ: АВ = DC = 9 см.
       ВС = AD = 18 см.

7. Постановка домашнего задания

Домашнее задание находится на столах учащихся на листах с напечатанными на них готовыми чертежами (смотри Приложение 2).
 

8. Подведение итогов урока

Учитель: «Итак, изучением какой темы мы с вами занимались на сегодняшнем уроке? А чем конкретно мы занимались, и что нам дал этот урок?»

Сообщаются оценки учащимся, отвечавшим на уроке.