В настоящее время большое внимание уделяется задачам оптимизации. В условиях ограниченности финансовых, природных и других ресурсов крайне остро стоит проблема их экономного использования. Борьба с пробками в крупных городах, разработка оптимального маршрута для перевозки грузов из-за Урала в Европейские регионы нашей страны, распределение нагрузки в электросети – все это примеры задач, где требуется применение методов оптимизации.

С одной стороны, такие задачи требуют аккуратной постановки с точки зрения физики и техники, с другой – довольно сложных математических методов. Решение таких задач школьниками кажется порой невозможным. Тем не менее, в простейших случаях такие задачи могут быть решены с использованием методов, вполне доступных и школьникам старших классов.

Как правило, задачи оптимизации содержат некоторый функционал, значение которого необходимо минимизировать (или напротив, максимизировать). Для этого в конечномерном случае находят нули частных производных, в бесконечномерном – решается уравнение Эйлера – Лагранжа [1]. В случае решения таких задач школьниками можно составить компьютерную программу, которая бы осуществляла перебор возможных значений и таким образом находила экстремальное значение функции. Наш опыт показывает, что написание программного кода для решения таких задач не только доступно школьникам, но и вызывает у них дополнительный интерес к изучению данной проблемы.

Мы провели со школьниками проектную работу, которая была посвящена решению важной практической задачи. Как известно, во многих городах-«миллионерах» имеются серьезные дорожные пробки. Бороться с ними можно различными способами. Один из самых популярных методов состоит в строительстве новых дорог. Тем не менее, опыт показывает, что это довольно дорого и малоэффективно. Еще один способ – строительство линий метрополитена или скоростного трамвая. Он весьма эффективен, но тоже крайне дорог. Наконец, опыт Москвы показал, что возможен одновременно низкозатратный и высокоэффективный путь, состоящий в организации скоростных маршрутов автобусов по выделенным полосам. Однако, чтобы такие маршруты пользовались популярностью, их прокладка требует крайне аккуратных оценок пассажиропотока. Решению этих задач для города Красноярска и была посвящена школьная проектная работа. Школьниками были проработаны несколько наиболее перспективных маршрутов, которые могли бы разгрузить транспортную систему данного города.

Проведение подобных работ требует от школьников знания математики в пределах курса общей школы и умения программировать в рамках курса информатики 8 – 9 классов.

Минимизация функций с помощью компьютера

В том случае, когда решается задача минимизации функции $U(x,y,...,z)$, в рамках вузовского курса она решается так: ищутся нули частных производных: $\frac{\partial U}{\partial x}=0, \frac{\partial U}{\partial y}=0, \dots, \frac{\partial U}{\partial z}=0$. Затем составляется второй дифференциал $d^2U$ и проверяется, будет ли он знакоопределенной квадратичной формой [2]. Если же функционал $U(f(x),p,q)$ содержит не только числовые параметры $p$ и $q$ но и неизвестную функцию $f(x)$ то задача поиска его экстремального значения еще более усложняется: например, в случае если функционал представляет собой интеграл, то приходится решать уравнение Эйлера – Лагранжа [1].

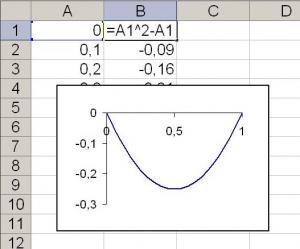
Все эти методы, конечно, являются крайне сложными для школьников, особенно 8 – 9 классов. Им неизвестно, что такое частные производные, а определение того, будет ли квадратичная форма знакоопределенной – и вовсе непосильный труд. Однако в курсе ИКТ школьники учатся составлению программ в рамках электронных таблиц Excel, которые можно применить для решения физических задач [3]. Попытаемся найти минимальное значение функции $f(x)=x^2-x$. Будем заносить в столбец A значения переменной $x$ в столбец B – значения функции $f(x)$. Заполним столбец А значения переменной $x$ от 0 до 1 с шагом 0.1, а столбец B – формулами, выражающими нашу функцию. Например, в ячейке B1 мы должны записать формулу: “=A1^2+A1”. Как непосредственное наблюдение значений, полученных во втором столбце, так и построенный график позволит школьникам определить, что минимальное значение функции находится в точке $x=0.5$.

Несколько более сложную задачу представляет собой нахождение минимума функции, зависящей от нескольких переменных. В таком случае использование таблиц Excel становится затруднительным. Для этого наиболее эффективный способ состоит в написании компьютерной программы. Она будет перебирать все возможные значения функции на заданном множестве и находить наименьшее из них.

Задача о создании оптимальных автобусных маршрутов в городе Красноярске

Изложенный выше метод решения задач оптимизации мы применяли для решения важной практической задачи об оптимальных интервалах для маршрутов автобуса в городе Красноярск. Данный город разделен рекой Енисей на две части, и каждое утро и вечер на подъездах к мостам скапливаются пробки [5]. Предполагается использовать опыт Москвы – ввести ускоренные маршруты автобусов по выделенным полосам.

Пусть расходы на топливо, зарплату водителя и амортизацию автобуса составляют соответственно $a, b$ и $c$ руб/км соответственно. (Эти данные возможно узнать из общедоступных технических характеристик популярных моделей, используемых в общественном транспорте.) Если протяженность маршрута составляет $l$ км, а общее число рейсов за время часа пик равно $K$ то расходы на работу маршрута составят $X=Kl(a+b+c)$Число рейсов можно оценить через интервал $m$ следующим образом: $K=\frac{120}{m}$.

Оценим теперь доходы от маршрута. При количестве пассажиров, равном $n$ и стоимости проезда, равной $q$ рублей, сбор с одного автобуса составит $\beta=nq$ рублей. Долю $\gamma$ пассажиров, которые воспользуются маршрутом, можно оценить так: пусть интервал движения существующих маршрутов будет равен $M$ а ускоренного маршрута - $m$ Тогда будем полагать, что $\gamma=\frac{M-m}{M}$ Если общее число пассажиров равно $P$ то сбор с маршрута за час пик составит $Y=\gamma q P$.

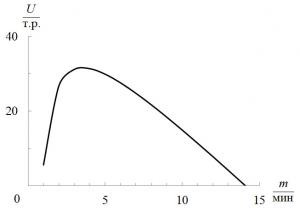
Чтобы найти оптимальные параметры, получим задачу максимизации функционала $U = Y-X$. Можно ввести зависимость от нескольких параметров и найти минимум соответствующей функции при помощи написанной школьниками программы. Пример зависимости от одной из переменных – интервала m – показан на рис. 1.

На основании работы данной программы нами были предложены следующие маршруты:

1. С1 «Центральный – Кировский», протяженность маршрута $2 \times 5$ км, оптимальный интервал – 2 минуты;
2. С2 «Центральный – Свердловский», протяженность маршрута $2 \times 13$ км, оптимальный интервал – 5 минут;
3. С3 «Центральный – Ленинский», протяженность маршрута $2 \times 7$ км, оптимальный интервал – 4 минуты.

Заключение

Нами было предложен метод решения задач оптимизации школьниками, который может быть основан на применении тех знаний, которые они получили в рамках школьного курса математики, физики и ИКТ. Одна из практически важных задач была решена нашим учеником и представлялась на Форуме Молодых Исследователей в рамках Фестиваля Науки МГУ в 2014 году.

В рамках предложенных методов можно предложить и другие возможные задачи, которые могут стать основой для выполнения школьных проектно-исследовательских работ. Например, можно предложить школьникам самостоятельно запрограммировать метод наименьших квадратов для обработки результатов физического эксперимента и получения параметров зависимости, отличающейся от линейной. Другой возможный вариант проектно-исследовательской работы – вычисление оптимального маршрута для грузов, движущихся из восточных районов нашей страны в Центральную Россию.

Работа была выполнена при поддержке программы «СТЕМ-центры» компании Intel. Автор выражает благодарность А.С. Морозову за ценные советы и помощь при проведении школьных исследовательских работ, а также коллективу ГБОУ СОШ №96 г. Москвы и в особенности И.М. Фатеевой.